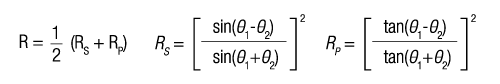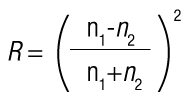Tech Notes » Reflection & Refraction of Light Tutorial
|
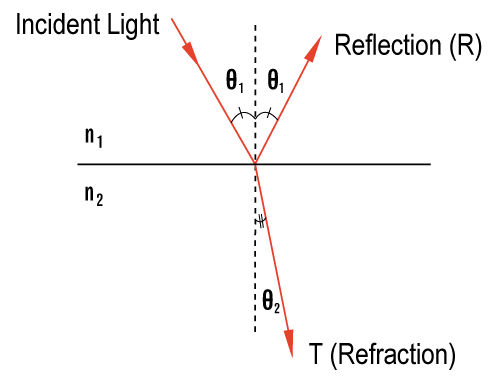
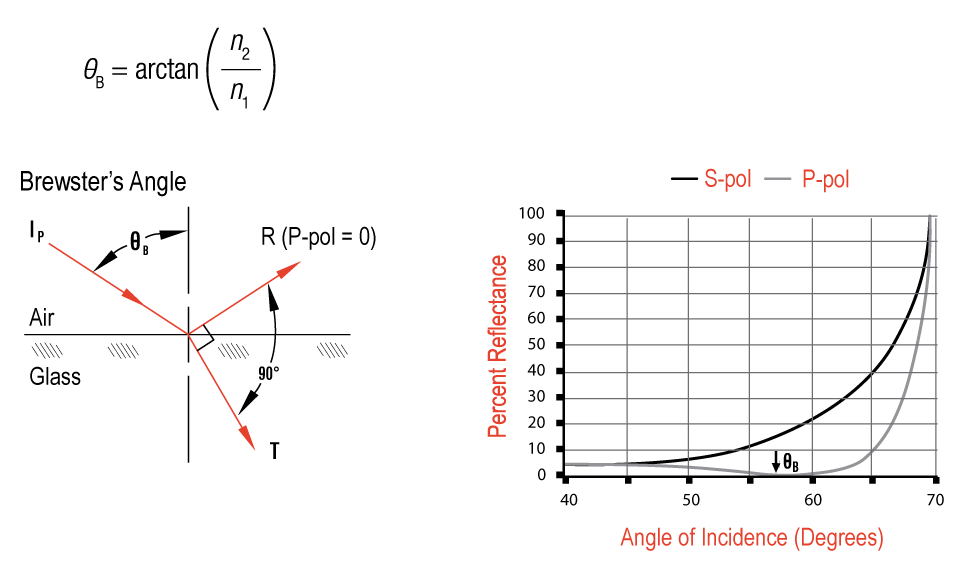
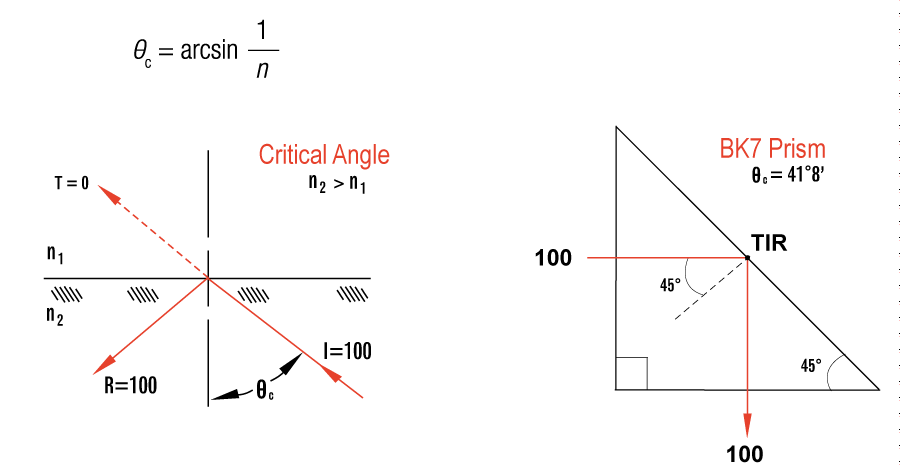
In this section, we will discuss some of the basic behaviors of light when it travels from one medium to another. We will also discuss two special cases, Brewster's Angle and the Critical Angle, which hae valuable applications in optics. Whenever an incident light traveling through one medium (ie: air with an index of refraction, denoted by "n", of 1) comes into contact with another medium with a high index of refraction (ie: glass with n=1.52), there is a reflected portion (bounces off the surface), and a refracted portion (transmits through the surface). There are three important considerations whenever this happens: |
||||||||||||||||||
|
1. What is the angle of refraction (θ2) relative to the incident (θ1) light? (It is generally known that the angle of reflection is equal to the angle of incidence). |
||||||||||||||||||
|
||||||||||||||||||